こんにちは。
みなさん、算数・数学は得意ですか？
僕は、めっちゃ嫌いです。
計算がとても苦手です。
でも、図形の面積などの公式はマスターしています。
公式を覚えるのがすごく苦手な人もいると思います。
では、どうしてあなたは公式を覚えるのが苦手なのか。
なぜ僕がこれほどに計算が苦手なのか。
二つに共通する答えは、「理解」です。
自分なりに理解できるまで、検索・練習をさぼってはいけません。
じゃあ、何を理解すればいいのか。
そこで今回説明するのは、
「テストに負けない公式の固め方。」です！
もくじ
1．覚え方より理屈。
皆さんは、平行四辺形の面積の求め方は知ってると思います。
もちろん、「底辺 × 高さ」ですよね。
じゃあ、どうしてそうなるか知っていますか？
これがすらりと言えるかどうかで
テストの算数で得られる点数に大きく差が付きます。
底辺×高さになる理由は…
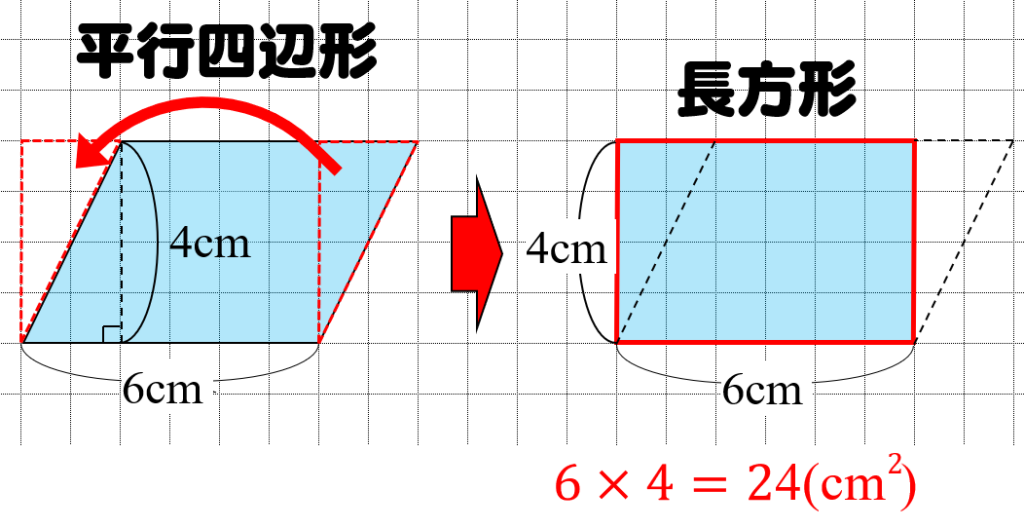
このように、どのような形でも、
長方形に直すことができます。
長方形の面積は、縦×横なので
底辺×高さでも、面積が求まるのです。
こんな感じで、すべての公式には理由があります。
それをしっかり理解すれば、公式なんて、
楽勝です。
だから、必ず理解しておく必要があるんです。
このように、たくさんの面積、周りの長さ等の求め方を
まとめてるので、ぜひ下のほうも見て行ってください。
公式をまとめる。
公式
四角形
公式）縦×横（1辺×1辺）
理由）マス目で考えると、
縦に何マス（何センチ）あるか？
縦が何列あるか？平行四辺形
公式）底辺×高さ
理由）１．に記載。三角形
公式）底辺×高さ÷2
理由）三角形を二つ重ねると平行四辺形になる。
平行四辺形の面積を求め、2で割れば三角形が出る。
円（面積）
公式）半径×半径×3.14
理由）
縦に何マス（何センチ）あるか？
縦が何列あるか？平行四辺形
公式）底辺×高さ
理由）１．に記載。三角形
公式）底辺×高さ÷2
理由）三角形を二つ重ねると平行四辺形になる。
平行四辺形の面積を求め、2で割れば三角形が出る。
円（面積）
公式）半径×半径×3.14
理由）
このように、円をいくつかに分けて、
長方形に変える。
このとき、半径が縦で、円周の半分の長さが横になる。
円周は直径×円周率（3.14）なので
半分は半径×円周率になる。
なので、半径×半径×円周率
（縦） （横）
となる。円（円周）
公式）直径×円周率
理由）円周率というのは、直径を何倍したら円周になるのかという
数なので、そのまま直径に円周率をかける。
台形
公式）（上底＋下底）×高さ÷2
理由）台形も、二つ重ねれば平行四辺形になります。
平行四辺形の底辺は、上の辺（上底）と、
下の辺（下底）を足したものです。
それに高さをかけ、平行四辺形の面積を求めてから、
２でわると、台形が求まります。
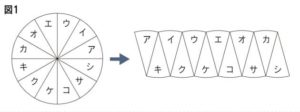
長方形に変える。
このとき、半径が縦で、円周の半分の長さが横になる。
円周は直径×円周率（3.14）なので
半分は半径×円周率になる。
なので、半径×半径×円周率
（縦） （横）
となる。円（円周）
公式）直径×円周率
理由）円周率というのは、直径を何倍したら円周になるのかという
数なので、そのまま直径に円周率をかける。
台形
公式）（上底＋下底）×高さ÷2
理由）台形も、二つ重ねれば平行四辺形になります。
平行四辺形の底辺は、上の辺（上底）と、
下の辺（下底）を足したものです。
それに高さをかけ、平行四辺形の面積を求めてから、
２でわると、台形が求まります。
ほかにも、「この公式はどうしてこうなの？」といった疑問は、
迷わず調べてください。
公式の理屈を覚えておくと、
周りの人の、半分ぐらいの時間で公式が覚えられます。
他の教科や、習い事などにたくさん時間を使うためにも、
公式なんて、すぐに終わらしてしまいましょう。
